Incompressible Navier-Stokes

In each time step, the incompressible Navier-Stokes equations are solved for the primitive variables velocity and pressure in a segregated manner by an iterative solution procedure.

Taylor-Couette flow

by: Thomas Utz, M.Sc.

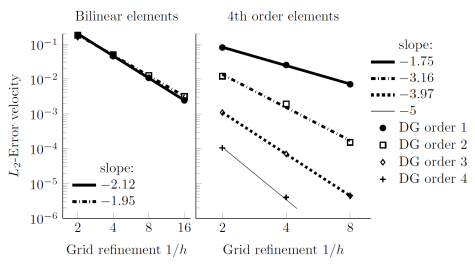
We study the planar Taylor-Couette flow, i.e. the flow between two rotating cylinders in the planar case. Without using curved elements at the boundaries, the convergence order of the numerical scheme is limited by the accuracy of the geometrical approximation. With curved elements, the scheme shows the desired convergence order of h^P+1:

taylor couette convergence — h-convergence for the two-dimensional Taylor-Couette flow: the convergence order is determined by both the approximation of the geometry and the flow field

In the 3D case, the flow becomes unstable and forms characteristic roll cells, as can be seen in the picture below. The low numerical dissipation of the high order Discontinuous Galerkin scheme allows for an accurate reproduction of the onset of instability, even on a coarse grid with 8 cells in radial direction.

Three-dimensional flow past a square cylinder

by: Dr.-Ing. Benedikt Klein

The three-dimensional flow past a square cylinder is simulated for Reynolds number Re = 300. A Cartesian grid with 32410 cells is used. Polynomial orders for velocity and pressure are 2 and 1, respectively. The time step size is set to Δt = 0.1 applying the BDF-2 scheme. The movie below shows iso-contours of the cross-stream vorticity.

Wall-mounted cube

by: Dr.-Ing. Florian Kummer

2D DNS of periodic channel

by: Dr.-Ing. Florian Kummer

A periodic channel was discretized by 256 × 144 Cartesian cells using 3rd polynomials. The simulation was performed on GPU cluster FUCHS using 4 MPI processes and 4 GPU’s.

Orr-Sommerfeld stability problem

by: Dr.-Ing. Benedikt Klein

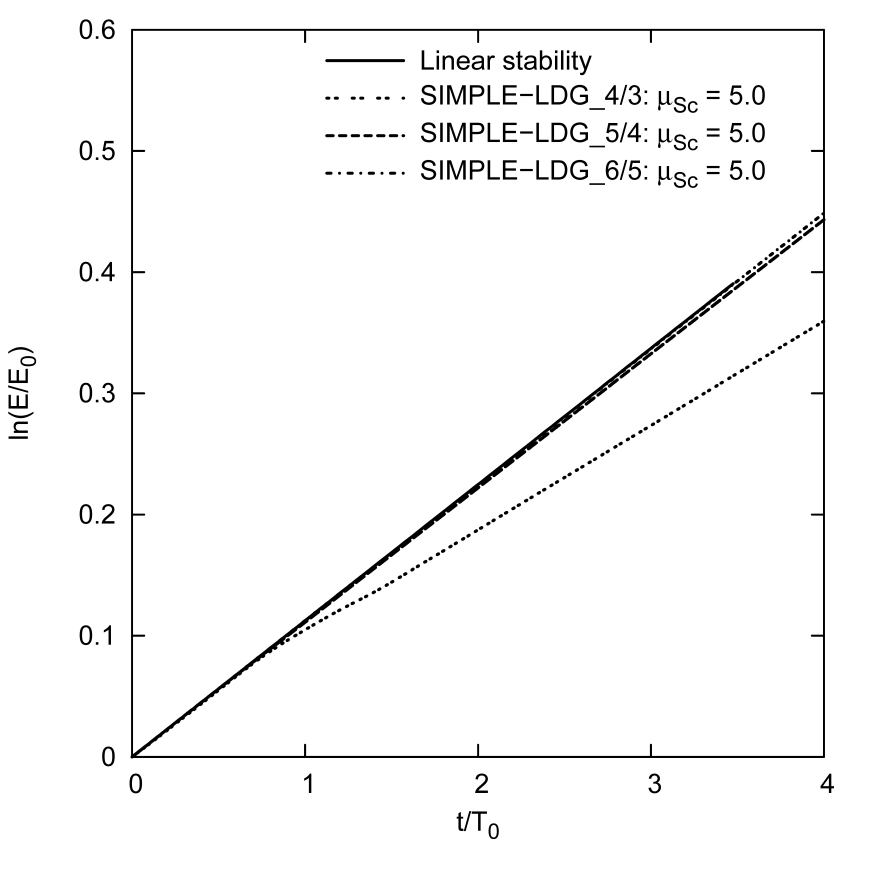
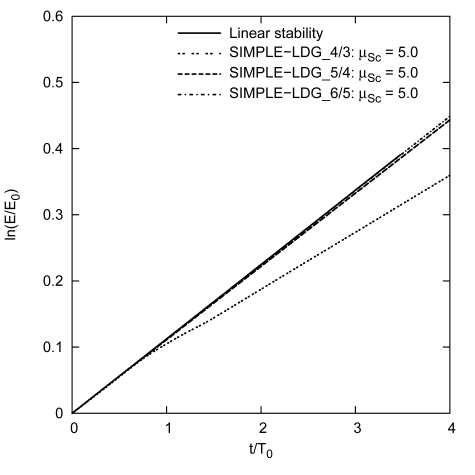
The stability of the solver is studied by simulating the Orr-Sommerfeld problem for a perturbed plane Poiseuille flow. Setting the Reynolds number to Re = 7500 and the wave number of the disturbances to α = 1, there is one unstable eigensolution.

orr_sommerfeld_ldg_energy — Peturbation energy vs. normalized time for the Orr-Sommerfeld stability problem applying various polynomial orders.

Taylor vortex flow

by: Dr.-Ing. Benedikt Klein

The Taylor vortex flow is studied for Re = 100. Time discretization is performed using the BDF-4 scheme with a time step size Δt = 0.01.

Incompressible Navier-Stokes

Taylor-Couette flow

Error on loading data

{{ year }}

Three-dimensional flow past a square cylinder

Error on loading data

{{ year }}

Wall-mounted cube

Error on loading data

{{ year }}

2D DNS of periodic channel

Error on loading data

{{ year }}

Orr-Sommerfeld stability problem

Error on loading data

{{ year }}

Taylor vortex flow

Error on loading data

{{ year }}